معادله درجه دوم:

·        تجزیه: سه جمله ای را به صورت حاصلضرب دو پرانتز تجزیه می کنیم و هر کدام را برابر صفر قرار می دهیم. سپس x را حساب می کنیم. (مثلا a×b=0 است؛ مطمئنا یکی از ایندو یا هر دوی آنها برابر صفر است.)

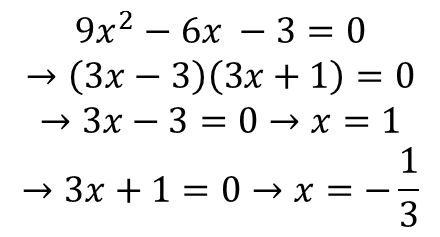
·        مربع کامل:

1. جملات مجهول را در یک طرف تساوی و عدد ثابت را طرف دیگر قرار می دهیم.

2. اگر ضریب x²غیر از یک است، طرفین را بر این ضریب تقسیم می کنیم.

3. مربع نصف ضریب x را به دو طرف معادله می افزاییم تا یک طرف مربع کامل شود.

4. در صورتی که دو طرف مثبت باشند از طرفین جذر می گیریم.

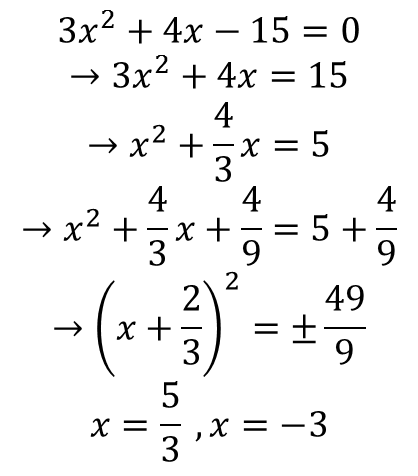
·        روش دلتا :

برای بدست آوردن دستور کلی معادله درجه دوم از روش مربع کامل کمک می گیریم.

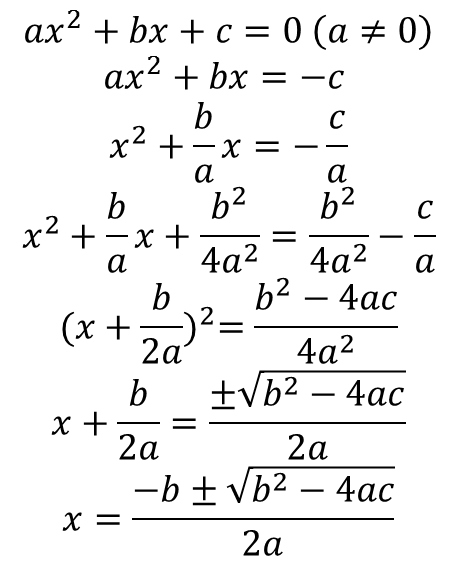
مبین معادله درجه دوم : عبارت b² - 4ac که ریشه های معادله ی درجه دوم ax² + bx +c به آن بستگی دارد و آن را مبین معادله گویند.

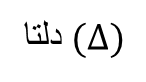
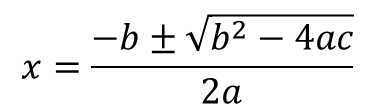
اگر دلتا > 0 باشد، معادله دارای دو ریشه حقیقی متمایز است.

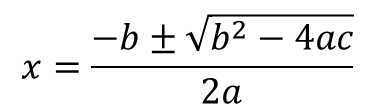
اگر دلتا = 0 باشد، معادله داری یک ریشه است و به آن ریشه مضاعف گویند.

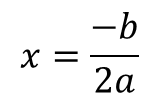
اگر دلتا < 0 باشد، معادله ریشه حقیقی ندارد.

مثال:

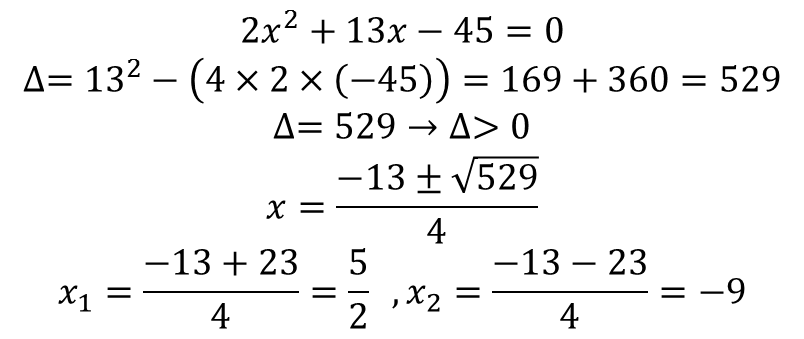
نکته:

در معادله ax² + bx + c اگر a و c علامت های مختلف داشته باشند، دلتا بیشتر از 0 است. این شرط برای وجود دو ریشه کافی است.

·        روش هندسی (سهمی): در آینده درباره این روش توضیح خواهیم داد.